2.16. Obsessed Tiler ¶

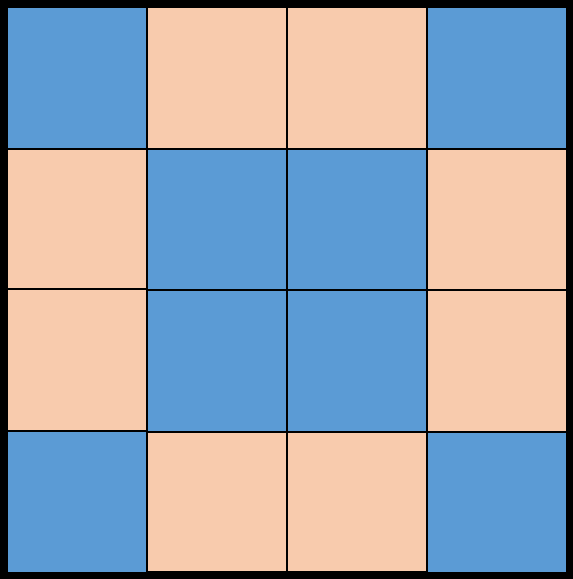
A tiler whose job is to tile the floor is obsessed with symmetry. The tiles that he is using are two colored squares of the same size. So, it is possible to represent the floor layout as a \(N\times N\) matrix with binary entries denoting the colors. An entry is either 1, for one type of the color or 0 for the other type of color.

For instance, the tile given in the figure above can be represented with the following list:

[[1, 0, 0, 1], [0, 1, 1, 0], [0, 1, 1, 0], [1, 0, 0 ,1]]

where 1 and 0 is representing the blue and light orange color respectively.

He wants to know whether a given tiling is diagonally (main diagonal) symmetric or not.

Write a program that determines whether the given tile is symmetric or not and prints True or False accordingly.

\(N\) can be any positive integer that is greater than or equal to 3.
Assume that the nested list of integers representing the tile will be given to you as variable \(\texttt{T}\).

Note that the earlier you detect the asymmetry, the more efficient program you get. So, try to write your code in the way that the outer loop is breakable as well.

Sample I/O:

Input:
[[1, 0, 0], [1, 0, 1], [1, 0, 1]]

Output:
False

Input:
T = [[1, 0, 1, 1], [0, 1, 0, 1], [1, 0, 1, 0], [1, 1, 0, 1]]

Output:
True

Input:
T = [[1, 0, 0, 1, 0], [0, 0, 0, 1, 1], [0, 0, 0, 1, 0], [1, 1, 1, 0, 1], [0, 1, 0, 1, 1]]

Output:
True

N = len(T)

result = True

for i in range(N):
     if not result:
         break

     for j in range(N):
         if T[i][j] != T[j][i]:
             result = False
             break

print(result)