2.17. Matrix Multiplication

Please refer the related section in textbook for the matrices, before reading this question.

Assume \(\mathbf{A}\) and \(\mathbf{B}\) are two matrices. If \(\mathbf{A}\) has dimensions \(m \mbox{(rows)} \times n \mbox{(columns)}\) and \(\mathbf{B}\) has dimensions \(n \mbox{(rows)} \times p \mbox{(columns)}\), then the product \(\mathbf{AB}\) is defined, and has dimensions \(m \mbox{(rows)}\times p \mbox{(columns)}\).

The entry \(\mathbf{(AB)}_{ij}\) is obtained by multiplying row \(i\) of \(\mathbf{A}\) by column \(j\) of \(\mathbf{B}\), which is done by multiplying corresponding entries together and then adding the results.

(2.17.1)\[\mathbf{(AB)}_{ij} = \sum_{k=1}^{n} \mathbf{A}_{ik}\times \mathbf{B}_{kj}\]

You shall note that matrix multiplication is not commutative (i.e. \(\mathbf{A} \times \mathbf{B}\) is not the same as \(\mathbf{B} \times \mathbf{A}\). It is quite possible that \(\mathbf{B} \times \mathbf{A}\) is not defined at all (due to row-column number mismatch))

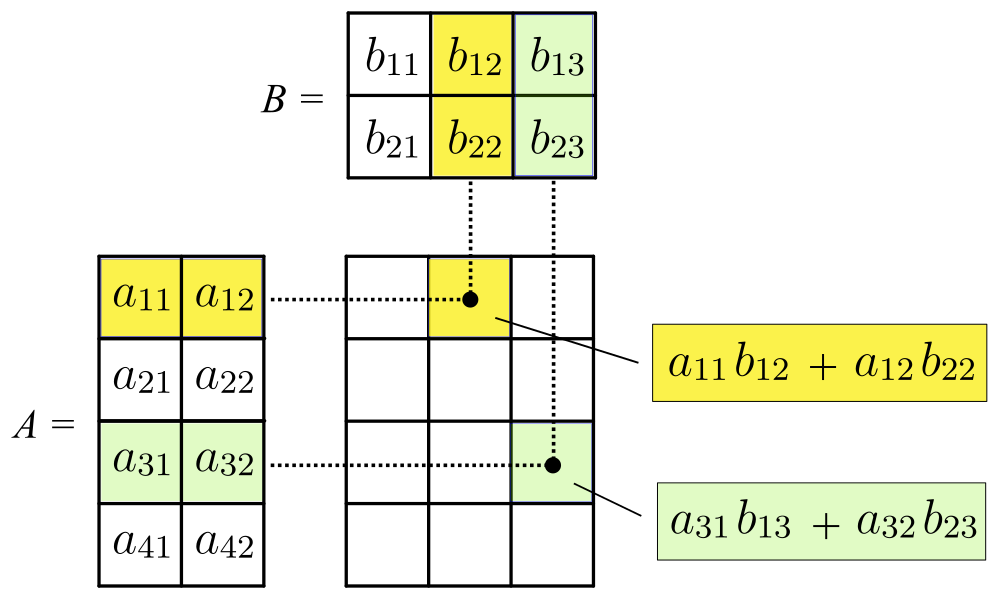
The figure above depicts an example operation of \(A \times B\).

You will practice matrix multiplication in this question. In python, we can have list of lists and we can think of them as matrices. The outermost list is holding the rows. So the first element is the first row, the second is the second row, and so on. Each row is represented by a list of its own. We can view this as the representation of a matrix. This list of lists, if stored into a variable s, can be indexed (like s[0][0], which will provide us the first item of the first list in s). s[1][4], for example, will stand for the the matrix element at the second row and the fifth column. Yes there is a clumsiness, list indexing starts with zero, matrix indexing start with 1.

So, having a Pythonic representation for matrices, by implementing the matrix multiplication rule above, we can do a matrix multiplication operation among two given matrices, in Python.

In this question, using the lines in the box below, you can read the list of lists, representing the matrices, conveniently into the variables matrix1 and matrix2. Then, you should do ‘matrix1 \(\times\) matrix2’ operation with your own programming skills. The result matrix must also be a two dimensional list and you can print this list variable directly as ‘print(result\(\_\)matrix)’.

Sample I/O:

Input:
[[12, 7, 3], [4, 5, 6], [7, 8, 9]]
[[5, 8, 1, 2], [6, 7, 3, 0], [4, 5, 9, 1]]

Output:
[[114, 160, 60, 27], [74, 97, 73, 14], [119, 157, 112, 23]]


Input:
[[1, 2], [2, 3]]
[[2, 2, 3], [4, 4 ,2]]

Output:
[[10, 10, 7], [16, 16, 12]]

Hint: In order to store correct values in the result matrix, you can create a two dimensional list full of 0’s by using list repetition.

Show the Answer

matrix1 = eval(input())
matrix2 = eval(input())

# Do not change the lines above

first_dimension_matrix1 = len(matrix1)
second_dimension_matrix2 = len(matrix2[0])
mutual_dimension = len(matrix2) # or it could be len(matrix1[0])
new_generated_matrix = [0] * first_dimension_matrix1
for i in range(first_dimension_matrix1):
    new_generated_matrix[i] = [0] * second_dimension_matrix2
for row in range(first_dimension_matrix1):
    for column in range(second_dimension_matrix2):
        for i in range(mutual_dimension):
            new_generated_matrix[row][column] += matrix1[row][i] * matrix2[i][column]

print(new_generated_matrix)